POPULATIONS (GÉNÉTIQUE DES)

POPULATIONS (GÉNÉTIQUE DES)

La génétique des populations est la discipline biologique qui étudie, au niveau collectif des populations d’organismes, les conséquences des trois propriétés fondamentales du matériel génétique: l’aptitude à la reproduction conforme, l’aptitude à être redistribué lors de la reproduction sexuée, l’aptitude à subir des mutations. Sous le nom de population, on désigne tout ensemble d’individus de même espèce cohabitant dans la même aire géographique et reliés génétiquement les uns aux autres. C’est essentiellement au cas des organismes à nombre chromosomique diploïde et à reproduction sexuée biparentale que s’intéresse la génétique des populations classique. La population est alors l’ensemble des individus à l’intérieur duquel s’opère systématiquement le choix des conjoints pour les actes reproducteurs qui assurent le passage d’une génération à la suivante, comme cela est réalisé pour la plupart des organismes supérieurs. Les organismes à reproduction exclusivement asexuée posent des problèmes très particuliers, non envisagés ici.

Malgré l’existence d’un important fond génétique commun, les individus d’une population ne sont presque jamais génétiquement identiques. Un même gène peut en effet exister dans une population sous la forme de plusieurs allèles. La description de cette diversité génétique, ou polymorphisme , utilise deux notions statistiques: les fréquences des génotypes diploïdes et les fréquences des gènes. Une première tâche de la génétique des populations est alors d’étudier les relations qui unissent les deux catégories de fréquences. Elles dépendent des règles statistiques qui président au choix des conjoints, qui se fera soit au hasard (panmixie), soit en fonction de certains critères introduisant des corrélations gamétiques (consanguinité et homogamie). D’autre part, les fréquences géniques sont soumises à des facteurs évolutifs dont le plus important est la sélection naturelle ; son étude purement mathématique conduit à la réalisation de modèles formels qui peuvent être comparés aux situations réelles observées dans la nature ou réalisées au laboratoire. Les mutations, autre facteur de variation des fréquences géniques, sont, bien entendu, la source ultime de toute diversité génétique; leur rôle immédiat, le plus facilement observable, est de maintenir en existence, dans les populations, des gènes que la sélection naturelle tend à éliminer.

Les fréquences géniques déterminées mathématiquement, compte tenu de l’action combinée de ces différents facteurs, ne sont valables que pour des effectifs très grands, pratiquement infinis. Quand le nombre des géniteurs d’une génération est faible, les hasards de la reproduction individuelle ne sont plus suffisamment amortis, et la composition génétique de la génération suivante n’est plus déterminée de façon stricte. Un élément purement aléatoire s’introduit dans la succession des générations et déplace la fréquence génique: on parle alors de dérive génétique .

La génétique des populations n’étudie donc que la structure génétique (aspect qualitatif) des populations, laissant l’étude de leur structure spatiale et de leurs fluctuations (aspect quantitatif) aux écologistes et éthologistes (cf. ÉCOLOGIE, ÉTHOLOGIE, SOCIÉTÉS ANIMALES). Les objets et les phénomènes qui relèvent de son domaine se prêtent assez aisément à une formulation mathématique abstraite. Celle-ci n’a cependant d’intérêt biologique que dans la mesure où il est possible de vérifier que les conclusions atteintes sont une description suffisamment fidèle des situations réelles.

1. Polymorphisme des populations naturelles

Les individus membres d’une même population, qui appartiennent à la même espèce, présentent toujours entre eux une ressemblance foncière. Celle-ci est à la base de la notion courante d’espèce et permet, le plus souvent sans grande difficulté, de classer et de désigner par son nom spécifique correct tout être vivant.

Cependant, cette ressemblance n’est, en aucun cas, une identité parfaite et la situation qui nous est familière dans l’espèce humaine, où l’individu est toujours identifiable à la fois en tant qu’individu et en tant que membre de la collectivité, existe en fait, à des degrés divers, chez tous les organismes.

Parmi les caractères qui permettent de distinguer les individus, c’est-à-dire le phénotype, certains sont uniquement liés aux stades de développement, telles les différences d’aspect en rapport avec l’âge. D’autres, en revanche, correspondent à des différences dans les génotypes individuels, et leur existence traduit ce que l’on appelle le polymorphisme de la population . Ce polymorphisme comporte diverses modalités. Il peut s’agir de variations dans l’aspect extérieur des individus: par exemple, variation de la coloration de la chevelure ou de l’iris dans l’espèce humaine; variation du plumage, gris ou roux, de la hulotte; variation de la couleur et de l’ornementation de la coquille du petit escargot des haies, Cepaea nemoralis (fig. 1). Chez les plantes, le polymorphisme peut affecter la couleur des fleurs, et c’est ainsi que chez la violette commune, Viola odorata , il n’est pas rare de rencontrer des pieds à fleurs blanches.

Il peut s’agir aussi de caractères physiologiques et biochimiques: l’espèce humaine fournit, avec les groupes sanguins, un exemple bien connu de cette situation. Outre le système A, B, O, qui comprend les quatre groupes classiques, on a pu identifier plusieurs autres systèmes indépendants qui correspondent, de la même manière, à la présence sur les hématies ou dans le sérum de substances à propriétés antigéniques différentes. En dehors des vrais jumeaux, il existe peu de chances de trouver deux individus possédant dans le sang strictement les mêmes antigènes, car la diversité des combinaisons possibles est quasiment infinie.

L’existence des groupes sanguins paraît limitée aux Vertébrés à sang chaud, mais une autre forme de polymorphisme biochimique semble tout à fait générale. Elle touche les molécules protéiniques qui, dans une espèce donnée, exercent une même fonction enzymatique. En utilisant les techniques actuelles qui permettent de distinguer avec précision les diverses espèces moléculaires de protéines, du fait notamment de leur mobilité dans un champ électrique, on s’aperçoit que, très souvent, une même enzyme existe dans les individus d’une population sous des formes moléculaires distinctes. Ces dernières correspondent à autant d’allèles du gène de structure de l’enzyme.

Enfin, dans certains cas, le polymorphisme intéresse la structure des chromosomes. Un exemple est connu chez une espèce de drosophile nord-américaine, Drosophila pseudoobscura , chez laquelle un même chromosome peut se rencontrer sous plusieurs types, qui diffèrent les uns des autres par des inversions: un segment de chromosome a subi un retournement de 180⁰ avant de se recoller aux segments terminaux ^{[cf. POLYMORPHISME BIOCHIMIQUE DES ÊTRES VIVANTS]}.

La description du polymorphisme d’une population conduit à définir trois catégories de fréquences. Les fréquences phénotypiques correspondent au groupement dans un même ensemble de tous les individus qui présentent le même phénotype; les fréquences des quatre groupes sanguins du système A, B, O en sont un exemple. Une deuxième catégorie de fréquences est établie avec les fréquences génotypiques ; dans le cas des groupes sanguins, on sait qu’il existe ainsi six génotypes qui correspondent à toutes les combinaisons, homozygotes et hétérozygotes, de trois allèles: I^O, I^A, I^B. Les groupes O et AB n’incluent chacun qu’un seul génotype, respectivement. Les fréquences de

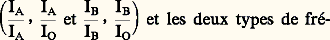ces génotypes sont alors égales aux fréquences phénotypiques correspondantes. En revanche, chacun des deux groupes A et B inclut deux génotypes distincts et les deux types de fréquences ne peuvent alors être confondus.

Pour définir la troisième catégorie, celle des fréquences géniques , ce ne sont plus les individus diploïdes qui sont considérés comme les unités dénombrables, mais les allèles présents dans leurs génotypes. En reprenant l’exemple des groupes sanguins, on définit les fréquences des trois allèles, I^A, I^B et I^O, dans la population.

2. Structure génétique d’une population

La structure génétique d’une population par rapport à une série de gènes allèles est définie lorsque l’on connaît les relations qui unissent les fréquences génotypiques aux fréquences géniques. Si, en effet, la connaissance des premières détermine entièrement celle des secondes, la réciproque n’est pas vraie. Ainsi, pour deux allèles a et a qui coexistent dans une population avec des fréquences respectives p et q = 1 漣 p , trois génotypes distincts peuvent être rencontrés, pour lesquels il existe a priori un nombre infini de jeux de fréquences compatibles avec la valeur p . Le jeu réalisé dans chaque cas particulier dépend des règles statistiques qui, lors du passage d’une génération à la suivante, interviennent dans le choix des conjoints.

La panmixie et la loi de Hardy-Weinberg

Très souvent, les unions se font au hasard, c’est-à-dire, plus précisément, qu’elles sont indépendantes aussi bien des génotypes (on dit qu’il y a absence d’homogamie) que des liens de parenté (absence de consanguinité). Cette situation correspond à ce que l’on appelle la panmixie . Il existe, dans ce cas, des relations simples (loi de Hardy-Weinberg), entre les fréquences p et q des deux allèles a et a et les fréquences des trois génotypes, qui sont p ² pour le génotype a/a , 2pq pour a/a et q ² pour a /a .

La démonstration que la panmixie aboutit effectivement à ce résultat est aisément apportée. Il suffit de remarquer que, dans une génération née de l’union au hasard des reproducteurs, tout se passe comme si chaque individu prenait naissance par le double tirage au sort de ses deux gamètes. Ce tirage se fait expérimentalement dans les deux cas, dans une urne où les deux types possibles a et a se rencontrent avec les fréquences p et q . Lorsqu’il existe plus de deux allèles, il suffit de considérer que l’urne contient plus de deux possibilités. La validité de la loi de Hardy-Weinberg est certainement très générale. De fait, dans la plupart des cas où la vérification a pu être faite, on s’est aperçu qu’effectivement les populations naturelles étaient sensiblement panmictiques (tabl. 1).

Quand il n’y a pas de dominance entre les allèles, les fréquences des génotypes peuvent être directement observées et permettent alors une vérification directe de la loi de Hardy-Weinberg. Dans le système de groupes sanguins M et N, il existe trois groupes qui correspondent aux trois génotypes possibles avec un couple de gènes allèles M et N. Sur 1 279 individus dénombrés en Angleterre, on en a trouvé 28,4 p. 100 du groupe M, 49,6 p. 100 de MN et 22,0 p. 100 de N.

On peut en déduire les fréquences des deux allèles:

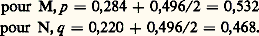La loi de Hardy-Weinberg conduit pour les fréquences des trois génotypes aux valeurs théoriques: p ² = 0,283, 2pq = 0,498 et q ² = 0,219, très proches des nombres effectivement observés.

Les fréquences données par la loi de Hardy-Weinberg correspondent à une situation stationnaire qui, en l’absence de facteurs faisant varier les fréquences géniques, est maintenue par la reproduction panmictique, génération après génération. Pour une seule série d’allèles, il suffit d’ailleurs d’un seul cycle de reproduction panmictique pour établir d’emblée les fréquences des génotypes aux niveaux prévus. Il n’en va plus de même lorsque l’on considère conjointement plusieurs couples ou séries d’allèles. Cela se produit, par exemple, lorsque des circonstances historiques amènent deux populations génétiquement distinctes à se fondre en une unique population panmictique; bien que, pour chaque série d’allèles, la loi de Hardy-Weinberg soit valable dès la première génération de panmixie, les associations de gènes présentes dans les deux groupes originels ne vont alors disparaître que progressivement. L’existence de liaisons génétiques (taux de crossing-over faibles) peut ralentir, mais non empêcher cette évolution.

L’homogamie

On parle d’homogamie lorsque, dans une population, le choix des conjoints ne s’opère plus au hasard, mais fait entrer en ligne de compte les ressemblances phénotypiques. Cette situation ne paraît pas très fréquente dans les populations naturelles, bien qu’elle existe à un certain degré dans l’espèce humaine (unions entre individus de taille voisine, par exemple). Dans la conduite des élevages d’animaux, par contre, on est souvent amené à ne retenir comme reproducteurs que les animaux présentant tel ou tel caractère désirable. Cela revient à imposer une homogamie qui peut être considérée comme une sélection artificielle.

La tendance modérée aux croisements homogamiques observée dans les populations humaines aboutit à réduire la fréquence des génotypes hétérozygotes par rapport à la situation qui correspondrait à la panmixie parfaite. On traduit ce fait en disant que l’homogamie, comme toutes les tendances qui s’écartent de la panmixie, introduit dans la population une corrélation gamétique . Avec une certaine probabilité, les deux gamètes qui s’unissent pour former un zygote ne résultent plus d’un double tirage au sort, mais sont choisis systématiquement identiques.

La consanguinité

Un croisement est qualifié de consanguin lorsque les conjoints sont plus ou moins étroitement apparentés. Tout ce qui, dans une population, favorise ce type d’union introduit une corrélation gamétique et tend donc à diminuer la fréquence des hétérozygotes.

Les unions consanguines qui se produisent occasionnellement à l’intérieur d’une population plus ou moins panmictique présentent un intérêt particulier. On peut définir pour un descendant d’une telle union un coefficient de consanguinité individuel , qui représente la probabilité pour que deux locus homologues, pris au hasard dans son génotype, soient occupés par deux gènes qui descendent l’un et l’autre d’un gène unique présent dans un ancêtre commun au père et à la mère. Ce coefficient F est, dans le cas d’un seul ancêtre commun, donné par l’expression:

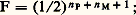n ^P et n ^M représentent le nombre de générations qui séparent respectivement le père et la mère de l’ancêtre (fig. 2). Ordinairement, il existe en fait plusieurs ancêtres communs au père et à la mère. Le coefficient de consanguinité est alors obtenu en faisant la somme de leurs contributions:

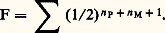Quand il s’agit d’un mariage entre cousins germains, l’application de cette expression conduit pour les descendants à la valeur F = 1/16. Le même coefficient serait de 1/8 pour un mariage entre oncle et nièce ou entre doubles cousins germains; il atteindrait 1/4 dans le cas d’une union entre frère et sœur.

Il est alors facile de montrer que, parmi les descendants de croisements consanguins, les fréquences des divers génotypes sont différentes de celles qui sont valables pour la population dans son ensemble. Les différences vont évidemment dans le sens d’un

accroissement des homozygotes. Si un couple d’allèles a et a existe avec des fréquences p et q , la fréquence des homozygotes a /a parmi les descendants de mariages entre cousins germains sera non plus p ², comme dans le cas de panmixie, mais (1 漣 F)p ² + Fp , c’est-à-dire p ² + Fpq , avec F égal à 1/16. Pour les faibles valeurs de p , on aboutira à un accroissement relatif énorme de la fréquence des homozygotes. Dans le cas, par exemple, d’un gène récessif responsable d’une tare héréditaire dont la fréquence est p = 1/200, la probabilité de naissance d’un enfant taré est de 1/40 000 pour un mariage quelconque; elle devient 1/3 200 environ dans le cas des mariages entre cousins germains.

La répétition systématique de croisements consanguins est une autre situation dont il est intéressant d’étudier les conséquences statistiques. Elle est en effet assez courante à la fois dans la nature et dans la pratique de l’élevage. C’est ainsi que, chez certaines espèces de végétaux supérieurs, l’autofécondation, forme extrême d’union consanguine, est systématique et peut même constituer la seule forme de reproduction sexuée spontanée. Dans le but d’obtenir des animaux d’aspect et de performances homogènes, les éleveurs ont souvent recours à une répétition systématique de croisements frère et sœur ou père et fille ^{[cf. ZOOTECHNIE]}.

Cette situation conduit plus ou moins rapidement à la disparition des génotypes hétérozygotes. Le coefficient de consanguinité individuel tend en effet vers l’unité au fur et à mesure que s’accumulent les ancêtres communs aux conjoints des croisements successifs. Si l’on prend, par exemple, à l’origine, une plante supposée hétérozygote pour un grand nombre de gènes, qui engendre par autofécondation des descendances successives, la fréquence de l’état hétérozygote pour un locus est divisée par deux à chaque génération. Chez les végétaux à autofécondation stricte (autogames), tels que le blé, la structure des populations est donc totalement différente de celle qui est caractéristique d’une espèce à sexes séparés, plus ou moins panmictique, comme l’espèce humaine. Toute population y est formée de lignées et, à l’intérieur de chaque lignée, les individus tendent à être génétiquement identiques ou homozygotes. Cependant, en raison de la production incessante de mutations, la parfaite homogénéité d’une lignée n’est jamais complètement atteinte.

De la même manière, la répétition de croisements consanguins moins stricts que l’autofécondation, par exemple de croisements frère et sœur, tend à fixer dans la famille un génotype homozygote. La fréquence des hétérozygotes décroît toutefois moins vite que dans le cas de l’autofécondation; elle est multipliée à chaque génération par un facteur qui est d’environ 0,81. C’est ainsi que dans la pratique de l’élevage sont obtenues les races pures. Si l’une d’elles est établie à partir d’une population originelle nombreuse, plus ou moins panmictique, elle tend à fixer un génotype homozygote qui, en l’absence de sélection, sera choisi au hasard parmi tous ceux que rend possibles le polymorphisme présent au départ.

3. Modifications des fréquences géniques

Rôle de la sélection naturelle

La sélection est l’un des facteurs importants du jeu desquels dépendent les fréquences des gènes. Ce facteur s’introduit par le fait que les individus de différents génotypes ne contribuent pas nécessairement de façon égale à la formation de la génération suivante. Deux facteurs de nature différente s’additionnent pour faire varier cette contribution: le premier est la probabilité de survie de l’individu au cours du développement qui le mène de l’œuf à l’âge reproducteur; le second est le taux de fécondité, une fois atteint l’âge de la reproduction. La valeur sélective globale d’un génotype est la résultante de ces deux éléments.

Mise en évidence

Que certains génotypes soient moins aptes que d’autres à survivre et à laisser une descendance est bien évident, pour l’espèce humaine, dans le cas des tares héréditaires graves telles que l’achondroplasie, l’idiotie amaurotique ou l’hémophilie. Chez toutes les espèces, on connaît également de nombreux gènes, souvent récessifs, qui sont qualifiés de létaux ou de sublétaux parce qu’ils interdisent ou rendent précaire la survie de l’individu.

L’action de la sélection au niveau de caractères qui ne sont pas aussi nettement monstrueux est par contre difficile à mettre en évidence. Une étude précise des populations naturelles est en effet toujours malaisée, ne serait-ce qu’en raison des délicats problèmes d’échantillonnage qu’elle soulève. Les facteurs qui, dans les conditions naturelles, agissent sur les populations pour en limiter l’effectif sont non seulement incontrôlables, mais le plus souvent même inconnus. La comparaison de deux génotypes ne peut en général être faite que pour un aspect fragmentaire de la valeur sélective, fécondité ou résistance à un prédateur, par exemple.

On peut, cependant, illustrer l’action de la sélection naturelle par de nombreuses observations portant sur des organismes divers. Les escargots des haies caractérisés par leur polymorphisme sont mangés par les grives, qui ont l’habitude de laisser sur des pierres les coquilles plus ou moins brisées des individus capturés. Dans une localité donnée, il est alors possible de comparer, au même moment, le nombre des individus mangés et celui des vivants. Il résulte d’une telle comparaison que parmi les deux phénotypes fondamentaux (coquilles unies sans bandes et coquilles avec bandes) c’est la première catégorie qui est plus fréquemment capturée par les oiseaux: les bandes sombres fonctionnent sans doute comme un camouflage (tabl. 2).

Une autre catégorie d’observations effectuées sur des organismes à plusieurs générations annuelles est relative à l’action des saisons sur la composition des populations. On peut en prendre pour exemple le polymorphisme chromosomique qui est observé chez Drosophila pseudoobscura : la fréquence d’une certaine inversion, dite ST, est de 30 p. 100 durant l’été, et de 70 p. 100 pendant l’automne (fig. 3). Une variation périodique des valeurs sélectives relatives des différents caryotypes est ainsi mise en évidence.

Les exemples qui viennent d’être cités correspondent à des situations où, globalement, l’action de la sélection présente un caractère conservateur (sélection conservatrice), puisqu’elle n’entraîne pas de changement à long terme dans les populations. Cela correspond à des cas où le milieu dans lequel vit l’espèce reste uniforme. S’il subit au contraire un changement, la sélection n’aura plus un caractère conservateur; son action va provoquer un changement durable dans la composition de la population.

Quelques exemples de ce type de phénomène ont pu être observés: l’un des plus célèbres concerne ce que l’on a appelé le mélanisme industriel des Lépidoptères. Il s’agit d’une transformation qui a atteint au cours du XIX^e siècle, dans les régions industrielles, les populations de certaines espèces de papillons, notamment la phalène du bouleau, Biston betularia . Il existe, chez cette espèce, une forme claire et une forme sombre, génétiquement contrôlées. Avant 1850, la variété noire était d’une extrême rareté, donc très recherchée des collectionneurs. Depuis cette date, elle est devenue de plus en plus courante, à tel point qu’elle a fini par envahir presque complètement, en remplaçant la forme claire, de nombreuses populations, en particulier toutes celles des régions les plus industrielles de la Grande-Bretagne. La forme claire est restée dominante dans les zones rurales occidentales, Cornouailles et Irlande notamment.

Il est apparu que l’élimination de la forme claire était liée à un phénomène de camouflage, en relation avec l’homochromie de l’insecte par rapport aux troncs sur lesquels il se repose pendant la journée. Les individus de couleur claire, difficilement repérables sur des troncs couverts de lichens, deviennent très visibles sur les troncs noircis par les fumées, d’où les lichens ont disparu. La situation est inverse pour la forme sombre. Des expériences directes de capture par les oiseaux ont permis de mettre en évidence d’une manière extrêmement frappante l’efficacité de ce camouflage.

Étude théorique

Comme beaucoup des phénomènes étudiés par la génétique des populations, l’action de la sélection est susceptible d’une formulation mathématique. En considérant le cas des trois génotypes a/a , a/a , et a /a , qui correspondent à un couple d’allèles, on peut représenter par les symboles 靖¹, 靖², 靖³ leurs valeurs sélectives respectives. Celles-ci tiennent compte à la fois de la probabilité de survie de l’individu et de son aptitude à laisser une descendance, une fois atteint l’âge adulte. Ces valeurs n’interviennent en fait que par leurs rapports, et l’une d’elles peut être choisie comme référence.

On peut alors facilement démontrer que, dans une population panmictique, la fréquence p de l’allèle a est modifiée par l’action de la sélection, en l’espace d’une génération, d’une quantité p , qui est donnée par l’expression:

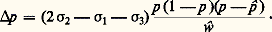dans laquelle:

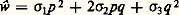et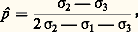

Il importe de distinguer deux catégories différentes de situations. Dans la première, les valeurs sélectives des différents génotypes en présence ne dépendent pas de leurs fréquences relatives: on parle alors de sélection à coefficients constants . Dans la seconde catégorie, ou sélection à coefficients variables , les coefficients 靖 sont au contraire dépendants de p , c’est-à-dire de la composition même de la population.

Lorsque c’est l’un des génotypes homozygotes qui présente la valeur sélective la plus élevée, toute sélection à coefficients constants tend évidemment à éliminer l’allèle défavorisé; elle est uniformisante. Au contraire, quand le génotype le plus favorisé est l’hétérozygote, la valeur p qui apparaît dans l’expression ci-dessus est comprise entre 0 et 1. Elle représente une position d’équilibre, pour laquelle s’annule l’action de la sélection sur la fréquence des gènes. La sélection est alors diversifiante ; elle aboutit à maintenir une diversité génétique.

Certains types de sélection à coefficients variables peuvent être diversifiants par un autre mécanisme que la valeur sélective préférentielle de l’hétérozygote. Cela se produit lorsque la rareté d’un génotype lui confère ipso facto une valeur sélective particulièrement élevée. On a observé qu’il en est ainsi dans la concurrence sexuelle chez la drosophile; mises en présence de plusieurs types génétiques de mâles, les femelles peuvent avoir tendance à choisir de préférence le type minoritaire.

Les sélections de type diversifiant sont certainement très fréquentes dans la nature. L’un des mécanismes qui conduit à cette situation, l’avantage de l’état hétérozygote, paraît être en effet très répandu. Dans le domaine de l’agronomie, le phénomène est bien connu et correspond à ce que l’on appelle la vigueur hybride. Pour obtenir aussi bien des plants de maïs vigoureux et productifs que des porcelets à croissance rapide, on recourt actuellement de façon systématique au croisement entre deux races pures.

Étude expérimentale

L’étude expérimentale de la sélection naturelle exige que soient réalisés des cultures ou des élevages dans des conditions difficiles à assurer parfaitement. Les populations doivent être nombreuses et les générations doivent se succéder à un rythme rapide. Il importe en outre que les conditions de vie offertes à l’organisme étudié soient voisines de celles du milieu naturel, en ce qui concerne notamment les possibilités de reproduction et d’installation des générations successives. À ce dernier point de vue, les végétaux constituent un matériel fort peu adéquat. Les expériences de Sukatchev sur le pissenlit ont pourtant montré l’existence de très nombreuses différences dans les caractères physiologiques des divers génotypes rencontrés dans les populations naturelles.

Comme pour la génétique formelle, ce sont les diverses espèces du genre drosophile qui ont fourni à la génétique des populations le matériel expérimental le plus commode. La technique utilisée est celle des cages à populations, ou démomètres, imaginées en 1933 par G. Teissier et P. L’Héritier, puis adoptées par T. Dobzhansky et son école. Il s’agit simplement de caisses, dans lesquelles on maintient en permanence une population de quelques milliers de drosophiles grâce à un renouvellement régulier des godets de nourriture dans lesquels se développent les larves. Le nombre d’œufs pondus sur chaque godet dépasse de plus de dix fois le nombre d’adultes finalement produits. La limitation de la nourriture établit donc entre les larves une compétition extrêmement sévère.

Dans les nombreuses expériences réalisées avec D. melanogaster , on peut observer, selon les gènes pris comme référence, soit des sélections uniformisantes, qui éliminent complètement l’allèle muté, soit des sélections qui maintiennent une population hétérogène (fig. 4). Ce dernier cas peut même concerner un gène létal à l’état homozygote, ce qui implique une nette supériorité de l’hétérozygote par rapport à l’homozygote normal.

On a pu étudier de même façon le polymorphisme de caryotypes de D. pseudoobscura . Comme dans la nature, certains types chromosomiques sont capables de coexister dans les élevages grâce à l’avantage sélectif présenté par certaines combinaisons hétérozygotes, ainsi que l’ont montré des mesures directes.

La technique des démomètres a permis de cerner aussi les facteurs dont peuvent dépendre les valeurs sélectives. Les conditions de milieu figurent parmi ces facteurs et l’influence de la température d’élevage a été mise en évidence notamment dans le cas des populations de D. pseudoobscura . De même on a montré que les valeurs sélectives attachées aux trois génotypes correspondant à un couple d’allèles peuvent dépendre du reste du génotype; c’est ainsi que chez D. melanogaster , l’équilibre entre le gène sépia et son allèle normal, qui s’établit aux environs de dix individus sépia pour cent sauvages, est de 30 p. 100 en présence d’un autre gène muté, le gène «vestigial».

Si la technique des cages à populations de drosophiles a permis quelques observations intéressantes, il importe toutefois de noter que les conditions d’élevage réalisées sont assez loin des conditions naturelles: la sélection ne joue dans ce cas que sur la fécondité des adultes et la concurrence pour l’alimentation entre larves. Dans la nature, bien d’autres éléments interviennent, tels que la résistance aux conditions climatiques extrêmes, l’aptitude à découvrir les milieux de ponte ou la capacité d’échapper aux agents microbiens pathogènes et aux prédateurs.

Rôle des mutations

On a considéré jusqu’ici les gènes comme ne subissant jamais aucun changement dans le passage d’une génération à la suivante. En raison du phénomène de mutation ^{[cf. MUTATIONS]}, cette stabilité n’est pas absolue: avec une probabilité qui reste toujours faible, un gène peut spontanément se transformer en un allèle.

Toute mutation individuelle se présente comme un accident rare, imprévisible; mais, si on considère pendant plusieurs générations consécutives une population nombreuse, on découvre qu’il se produit nécessairement un grand nombre de ces accidents à chaque cycle de reproduction. Pour estimer l’importance du phénomène, il importe de connaître les taux de mutation.

Un taux de mutation définit, en principe, la probabilité pour qu’un allèle déterminé se transforme en un autre durant l’intervalle de temps qui sépare deux générations. On sait toutefois qu’il existe un nombre très élevé d’allèles d’un même gène ^{[cf. GÉNÉTIQUE]}. Dans le domaine de la génétique des populations, on est de la sorte amené à grouper en quelques classes ces nombreux allèles, groupement évidemment fondé sur l’effet phénotypique. Les taux de mutation envisagés correspondent alors aux transformations spontanées qui font passer le gène d’une classe dans l’autre. Dans ce qui suit, on ne considérera que deux classes d’allèles, désignées par les symboles a et a ; le taux de mutation de a vers a sera représenté par u et le taux de la mutation inverse par v .

Bien que, en dernière analyse, la responsabilité de toute variabilité génétique incombe aux mutations, celles-ci n’exercent à l’échelle immédiate qu’une action faible sur les fréquences géniques. Les taux de mutation atteignent 10 size=1^漣4 ou 10 size=1^漣5 dans l’espèce humaine et sont encore plus faibles chez la drosophile, dont les générations sont bien plus courtes.

Si p et q représentent les fréquences des classes d’allèles a et a , la variation provoquée par les seules mutations dans le passage à la génération suivante est donnée par l’expression: p = 漣 up + 益 (1 漣 p ) qui, en toutes circonstances, correspond à une valeur très faible.

Dans le cas où les mutations interviendraient seules, la population devrait tendre à se fixer sur une position d’équilibre: p = 益/(u + 益). Il est en fait douteux qu’un semblable équilibre puisse réellement exister dans la nature. D’une part, en effet, l’absence de toute force de sélection est une hypothèse improbable et, d’autre part, le retour vers l’équilibre est tellement lent que tout déplacement accidentel exigerait des centaines, sinon des milliers de générations pour être rattrapé. Il est plus réaliste d’envisager l’action simultanée des mutations et de la sélection naturelle.

S’il s’agit d’une sélection diversifiante, l’action des mutations se borne à déplacer légèrement les équilibres de fréquences géniques commandés par les forces de sélection. Le cas intéressant est celui des sélections uniformisantes. Grâce aux mutations, les allèles désavantageux ne seront pas totalement éliminés par la sélection et tendront à persister avec des fréquences faibles, au niveau desquelles s’équilibrent leur production continuelle par mutations et leur élimination sélective.

Des valeurs approximatives des positions d’équilibre sont fournies par des expressions très simples. Il faut distinguer deux cas: celui où l’allèle défavorisé, désigné par a , est dominant: ( 靖¹ 礪 靖² 閭 靖³) et celui où il est récessif: ( 靖¹ = 靖² 礪 靖³). On peut montrer que les fréquences d’équilibre q sont alors respectivement:

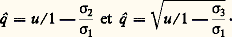Le fardeau génétique

Grâce au jeu combiné des mutations et de la sélection naturelle, un nombre considérable de gènes défavorables, dont beaucoup sont létaux ou sublétaux à l’état homozygote, persistent à une fréquence faible dans toute population. L’expression de «fardeau génétique» (genetic load ), introduite par H. J. Muller, désigne l’ensemble de ces gènes, qui sont responsables de l’apparition à chaque génération d’un certain contingent d’anormaux génétiques.

La plus grande partie du fardeau génétique est constituée par des gènes récessifs. Il est apparent, en effet, d’après les expressions ci-dessus, que, à désavantage sélectif comparable, un gène récessif se stabilise à une fréquence bien plus élevée qu’un gène dominant.

L’importance globale du fardeau génétique est proportionnelle à la production des mutations et inversement proportionnelle à l’intensité de la sélection. Or, dans les conditions où vit l’humanité moderne, d’une part, les taux de mutations risquent d’être augmentés par l’utilisation des rayons X et de l’énergie atomique et par la pollution chimique de l’environnement, d’autre part, les progrès de l’hygiène et de la médecine ont pour résultat de diminuer l’intensité de la sélection. Il est donc peu douteux que le fardeau génétique de l’espèce humaine ne soit actuellement en augmentation. C’est là un très grave problème que les hommes devront tôt ou tard affronter.

4. La dérive génétique

Le jeu combiné de la sélection et des mutations tend donc à fixer les fréquences géniques sur des positions d’équilibre. Même dans des conditions supposées parfaitement constantes, ces équilibres ne sont en fait réellement maintenus sans changement d’une génération à l’autre que si l’effectif de la population est extrêmement grand, illimité en principe. La limitation de l’effectif des reproducteurs introduit toujours, en effet, une tendance à une variation aléatoire des fréquences géniques au cours de la succession des générations. Ce phénomène a reçu le nom de dérive génétique.

Étude théorique

Lorsque l’effectif de la population est limité, le niveau unique d’équilibre d’un gène a est remplacé par le jeu des probabilités avec lesquelles peuvent être réalisées les différentes fréquences. Ainsi que l’a montré Sewall Wright, ces probabilités correspondent sensiblement à la loi de distribution traduite par l’expression suivante:

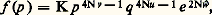où p et q sont les fréquences relatives des deux classes d’allèles a et a , u et v les taux de mutation de a vers a et de a vers a , N l’effectif des reproducteurs, et w la valeur sélective moyenne de la population supposée panmictique, donnée par l’expression:

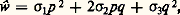dans laquelle les symboles 靖 représentent les valeurs sélectives des trois génotypes a/a , a/a et a /a . Cette loi de distribution correspond à un état stationnaire qui serait maintenu, génération après génération, par une quantité illimitée de populations supposées toutes de même effectif et soumises aux mêmes conditions.

Un aspect essentiel des courbes représentant l’équation de Wright (fig. 5) est qu’elles changent de forme selon le signe des exposants de p et de q . Or les quantités 2Nv et 2Nu représentent les productions globales de gènes a ou de gènes a par des populations pures pour l’autre allèle. Lorsque ces productions sont faibles, cas des petites populations, les états homoalléliques, p = 0 et p = 1, sont des situations très probables. Leur probabilité de réalisation est au contraire faible ou même nulle, lorsque les productions de gènes nouveaux ont dépassé un seuil critique. Pour diverses raisons, le seuil est toutefois moins brutal dans la réalité qu’il n’apparaît sur l’expression mathématique.

Formation des isolats

La plupart des espèces sont représentées, à chaque génération, par un nombre considérable d’individus. Il est cependant relativement exceptionnel que ceux-ci forment une population unique que l’on puisse considérer comme panmictique, même approximativement. Dans la situation la plus courante, l’espèce est fragmentée en un certain nombre de groupes ou isolats , au sein desquels reste plus ou moins strictement confiné le choix des conjoints. Le nombre et l’importance de ces isolats, l’étendue des aires géographiques qu’ils occupent et la rigueur de leur séparation sont, bien entendu, infiniment variés selon les cas et les types d’organismes.

De toute façon, une règle constante est que les isolats d’une même espèce présentent un certain nombre de différences génétiques. Cela reste vrai même lorsque l’isolement n’est pas absolu et qu’un courant d’échanges génétiques est entretenu par la migration, à chaque génération, de quelques individus d’un isolat vers l’autre.

Lorsque les conditions de vie ne sont pas strictement les mêmes pour divers isolats d’une même espèce, la sélection peut être l’un des facteurs responsables des différences génétiques qui s’établissent entre eux. Mais, même lorsqu’il n’en est pas ainsi, la dérive suffit pour aboutir à ce résultat. Le passage par pure dérive d’un état homoallélique à l’autre est évidemment un événement rare au niveau d’un seul couple d’allèles, mais, étant donné que le patrimoine génétique d’une espèce est formé d’un nombre énorme de gènes, cet événement rare se réalise toujours pour quelques-uns des locus. Dès qu’une population cesse d’être très importante, il se produit donc obligatoirement des variations notables de la composition génique: certains allèles seront éliminés tandis que d’autres seront fixés à l’état homoallélique.

La tendance des isolats d’une même espèce à se diversifier par le simple jeu de la dérive génétique peut entraîner d’ailleurs par contrecoup une action également diversifiante de la sélection. Les valeurs sélectives des différents génotypes possibles au niveau d’un locus dépendent en effet du contexte génétique; elles peuvent donc changer à la suite d’une modification de celui-ci.

Le principe des fondateurs

Bien entendu, la tendance d’un isolat à acquérir par dérive une composition génique particulière est d’autant plus accentuée que l’effectif est plus limité. Une occasion propice à cette diversification correspond à la fondation d’une population nouvelle isolée, par exemple d’une population insulaire, à partir d’un nombre restreint d’individus. Cette population présentera vraisemblablement des caractères bien différents de ceux de la souche d’origine des fondateurs. La différence initiale qui résulte de ceux-ci risque fort, en effet, d’être le point de départ d’un processus irréversible de divergence.

Comme le type d’événement qui aboutit à ce résultat a dû se produire bien des fois au cours de l’histoire de la biosphère, il revêt un intérêt particulier au point de vue de l’interprétation de l’évolution. Le phénomène est connu sous le nom de principe des fondateurs.

Le principe des fondateurs a pu être observé en cages à populations avec l’espèce Drosophila pseudoobscura . Lorsque, dans un démomètre, on introduit à l’origine deux types chromosomiques, un équilibre stationnaire s’établit entre eux au bout de quelques générations. Le niveau de cet équilibre est variable et dépend en fait du contexte génétique apporté par les fondateurs choisis. Au cours d’une expérience, deux séries de démomètres ont été comparées. Dans la première, les populations ont été fondées avec un nombre important d’individus; dans la seconde, elles l’ont été avec un nombre plus restreint. Or, c’est dans la seconde série que les niveaux d’équilibre atteints étaient, et de beaucoup, les plus dispersés (fig. 6).

5. Domaines d’application

De toutes les branches de la génétique, la génétique des populations est l’une de celles qui trouvent le plus d’applications pratiques. Elles se situent essentiellement dans deux domaines: médical et agronomique.

La génétique des populations s’introduit dans le domaine médical avec la reconnaissance des tares héréditaires, dont l’ensemble forme le fardeau génétique de l’espèce humaine. La connaissance de la nature et de l’origine de ce fardeau et celle des règles auxquelles obéit sa répartition à chaque génération, celles notamment qui concernent l’influence des mariages consanguins, constituent un point de départ indispensable pour envisager les mesures sociales propres à l’alléger.

Dans le domaine agronomique, la création, chez les plantes cultivées ou les animaux domestiques, de types génétiques mieux adaptés à l’économie moderne nécessite évidemment la connaissance des lois de la génétique formelle, mais fait également intervenir les notions étudiées par la génétique des populations. Les opérations couramment pratiquées par les agriculteurs ou les éleveurs, telles que le recours aux croisements consanguins ou homogamiques et la sélection artificielle, relèvent directement du champ d’étude de cette discipline.

Dans le domaine de la connaissance fondamentale, le problème auquel la génétique des populations apporte une contribution capitale est celui des mécanismes de l’évolution biologique. Si, comme le pense la majorité des biologistes, les transformations évolutives n’ont fait entrer en jeu que les propriétés des organismes que l’on peut observer, c’est évidemment en extrapolant à partir de ce qui est connu de la structure des populations et de leurs transformations récentes que l’on peut espérer comprendre ce qui s’est passé au cours de la longue histoire de la vie sur la Terre. Il importe toutefois, pour pouvoir rendre compte des transformations évolutives, d’étendre le domaine de la génétique des populations, tel qu’il a été défini plus haut, à l’étude du processus de formation des espèces ou spéciation ^{[cf. SPÉCIATION]}.

Encyclopédie Universelle. 2012.